문제 링크:
난이도: 골드 3
문제:
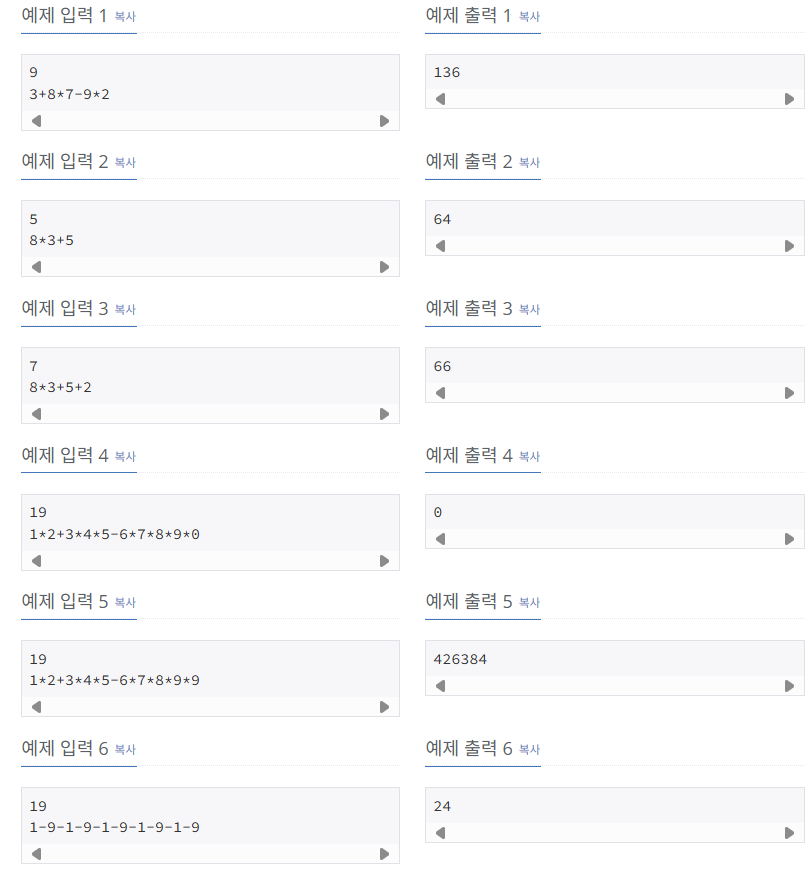
길이가 N인 수식이 있다. 수식은 0보다 크거나 같고, 9보다 작거나 같은 정수와 연산자(+, -, ×)로 이루어져 있다. 연산자 우선순위는 모두 동일하기 때문에, 수식을 계산할 때는 왼쪽에서부터 순서대로 계산해야 한다. 예를 들어, 3+8×7-9×2의 결과는 136이다.
수식에 괄호를 추가하면, 괄호 안에 들어있는 식은 먼저 계산해야 한다. 단, 괄호 안에는 연산자가 하나만 들어 있어야 한다. 예를 들어, 3+8×7-9×2에 괄호를 3+(8×7)-(9×2)와 같이 추가했으면, 식의 결과는 41이 된다. 하지만, 중첩된 괄호는 사용할 수 없다. 즉, 3+((8×7)-9)×2, 3+((8×7)-(9×2))은 모두 괄호 안에 괄호가 있기 때문에, 올바른 식이 아니다.
수식이 주어졌을 때, 괄호를 적절히 추가해 만들 수 있는 식의 결과의 최댓값을 구하는 프로그램을 작성하시오. 추가하는 괄호 개수의 제한은 없으며, 추가하지 않아도 된다.
입력:
첫째 줄에 수식의 길이 N(1 ≤ N ≤ 19)가 주어진다. 둘째 줄에는 수식이 주어진다. 수식에 포함된 정수는 모두 0보다 크거나 같고, 9보다 작거나 같다. 문자열은 정수로 시작하고, 연산자와 정수가 번갈아가면서 나온다. 연산자는 +, -, * 중 하나이다. 여기서 *는 곱하기 연산을 나타내는 × 연산이다. 항상 올바른 수식만 주어지기 때문에, N은 홀수이다.
출력:
첫째 줄에 괄호를 적절히 추가해서 얻을 수 있는 결과의 최댓값을 출력한다. 정답은 231보다 작고, -231보다 크다.
문제이해:
이 문제는 +, -, * 의 연산 우선순위가 모두 동일한 수식이 주어졌을 때 괄호를 적절히 배치하여 만들 수 있는 값 중 최댓값을 구하는 문제이다. 괄호는 반드시 연산자 하나만 포함해야 하며, 괄호 안에 괄호를 다시 넣는 중첩은 허용되지 않는다. 예를 들어 (3+2)는 가능하지만 (3+2+9)는 불가능하다.
예제 입력 3인 8*3+5+2를 보면, 괄호를 사용하지 않고 계산하면 ((8*3)+5)+2 = 31이 된다. 그러나 8*(3+5)+2와 같이 괄호를 배치하면 결과가 66이 되어 더 큰 값을 얻을 수 있다. 따라서 이 경우 정답은 66이 된다.
구현 방향:
이 문제를 해결하기 위해서는 수식의 처음부터 끝까지 모든 경우를 재귀적으로 탐색해야 한다.
각 연산자 위치에서 괄호를 사용하지 않는 경우와 괄호를 사용하는 경우로 나누어 계산하며, 모든 가능한 식의 결과를 구한 뒤 그 중 최댓값을 선택한다.
괄호를 사용하지 않는 경우에는 현재까지의 누적값과 다음 숫자를 단순히 연산한다.
괄호를 사용하는 경우에는 다음 연산자와 그 양쪽 숫자를 먼저 묶어 계산한 뒤, 그 결과를 현재까지의 누적값과 연산한다. 이렇게 분기를 따라가며 깊이 우선 탐색(DFS)을 수행하면, 자연스럽게 모든 괄호 배치를 고려할 수 있다.
예제 입력 1을 예로 들어보자 dfs(index,sum)이다.
dfs(0,3)
├─ 괄호X → dfs(1,11)
│ ├─ 괄호X → dfs(2,77)
│ │ ├─ 괄호X → dfs(3,68) → dfs(4,136)
│ │ └─ 괄호O → dfs(4,59)
│ └─ 괄호O → dfs(3,-22) ...
└─ 괄호O → dfs(2,59)
├─ 괄호X → ...
└─ 괄호O → ...이처럼 각 단계에서 괄호를 쓰는 경우와 쓰지 않는 경우로 분기하며 끝까지 탐색하고, 모든 결과 중 최댓값을 선택하는 것이 문제 해결의 핵심이다.
이를 코드로 그대로 구현하면 다음과 같다.
정답코드:
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
static int size;
static char[] oper;
static int [] number;
static int numCnt=0;
static int opCnt=0;
static int max = Integer.MIN_VALUE;
public static int cal(char oper, int num1, int num2){
switch (oper) {
case '+':
return num1 + num2;
case '-':
return num1 - num2;
case '*':
return num1 * num2;
}
return -1;
}
public static int dfs(int idx,int sum){
if (idx == opCnt) {
max = Math.max(max, sum);
return sum;
}
//괄호가 없는 경우
int result= cal(oper[idx], sum,number[idx+1]);
dfs(idx+1,result);
//괄호가 있는 경우
if (idx + 1 < opCnt) {
int bracket = cal(oper[idx + 1], number[idx + 1], number[idx + 2]);
int next2 = cal(oper[idx], sum, bracket);
dfs(idx + 2, next2);
}
return max;
}
public static void main(String[] args) throws IOException {
//초기 세팅
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
size=Integer.parseInt(br.readLine());
oper=new char[size/2];
number=new int[size/2+1];
String str= br.readLine();
StringBuilder sb=new StringBuilder(str);
for(int i=0; i<size; i++){
//홀수면 숫자
if(i%2==0){
number[numCnt++]= sb.charAt(i) -'0';
}
else{
oper[opCnt++]=sb.charAt(i);
}
}
//초기세팅 끝
//처음부터 탐색 시작
int result = dfs(0, number[0]);
//결과 출력
System.out.println(result);
}
}
마무리하며:
처음 이 문제를 접했을 때는 괄호를 어떻게 배치해야 하는지를 코드로 구현하는 방법이 잘 떠오르지 않아 꽤 막막했다.
그래서 여러 블로그를 참고하며 아이디어를 정리했고, 그 과정을 통해서야 비로소 구조를 잡을 수 있었다. 완성된 코드를 다시 보면 “괄호를 쓰는 경우와 쓰지 않는 경우로 나누어 DFS로 모든 경우를 탐색한다”라는 단순한 원리로 정리되지만, 직접 구현하는 과정에서는 인덱스 처리나 누적 값 관리처럼 신경 써야 할 세부 사항이 많아 쉽지 않았다.
결국엔 시행착오를 거쳐 풀어냈지만, 구현 과정에서 느낀 어려움 덕분에 완전탐색과 DFS에 대해 더 깊이 이해할 수 있었던 문제였다.
'코딩 테스트' 카테고리의 다른 글
| [백준] 13913 숨바꼭질 4 (JAVA) (0) | 2025.09.19 |
|---|---|
| [백준] 12851 숨바꼭질 2 (JAVA) (0) | 2025.09.18 |
| [백준] 12869 뮤탈리스크 (JAVA) (2) | 2025.09.15 |
| [백준] 4179 불! (JAVA) (0) | 2025.09.15 |
| [백준] 16234 인구이동 (JAVA) (0) | 2025.09.13 |
