자바에서 배열은 가장 손쉽게 데이터를 담는 방법이다. new String[5]처럼 선언 한 번으로 바로 메모리를 잡아주고, arr[2]로 빠르게 요소를 꺼낼 수 있다. 그러나 실제 서비스 규모가 커지면 배열의 한계가 금세 드러난다.
예를 들어 주문 내역을 배열에 담아 관리한다고 가정하자. “최대 10만 건”이라 미리 크기를 잡아두었는데, 주문량이 15만 건으로 늘어나면 새 배열을 만들고 기존 데이터를 전부 복사해야 한다. 이 과정은 O(n)의 시간이 들기 때문에, n이 커질수록 서버 부담이 커진다. 반대로 주문량이 적으면 사용되지 않는 공간이 낭비된다. 중간에 어떤 주문을 삭제해야 할 때는 그 뒤의 모든 요소를 한 칸씩 앞으로 당겨야 한다. 천만 건 단위라면 삭제 한 번에 천만 번 이상의 대입 연산이 발생하는 셈이다.
이처럼 배열의 ‘크기 고정’, ‘중간 삽입·삭제 비효율’, ‘메모리 복사 비용’ 문제를 해결하기 위해 자바는 ArrayList와 LinkedList를 제공한다. 다음 두 구현체를 직접 만들어 보며, 각 구조가 어떻게 동작하고 언제 어떤 리스트를 선택해야 부담을 줄일 수 있는지 살펴볼 것이다.
MyArrayList: 배열 기반 리스트의 내부 구조 구현
ArrayList는 내부에 배열을 유지하다가 요소가 가득 차면 두 배로 늘리고, 인덱스 기반 접근은 그대로 O(1)을 유지한다. 중간 삽입·삭제에는 여전히 배열 요소 이동 비용이 발생한다.
구현 코드:
package collection.array;
import java.util.Arrays;
public class MyArrayList<E> {
private static final int DEFAULT_CAPACITY = 5;
private Object[] elementData; // 내부 배열
private int size = 0; // 실제 요소 개수
// 생성자는 제네릭 배열을 만들 수 없으므로 Object[]를 사용한다.
public MyArrayList() {
elementData = new Object[DEFAULT_CAPACITY];
}
public MyArrayList(int initialCapacity) {
elementData = new Object[initialCapacity];
}
// 맨 뒤에 요소를 추가한다. 배열이 꽉 차면 길이를 두 배로 확장한다.
public void add(E e) {
if (size == elementData.length) {
elementData = Arrays.copyOf(elementData, elementData.length * 2);
}
elementData[size++] = e;
}
// 지정한 위치에 요소를 삽입한다. 삽입 지점부터 끝까지 한 칸씩 뒤로 민다.
public void add(int index, E e) {
if (size == elementData.length) {
elementData = Arrays.copyOf(elementData, elementData.length * 2);
}
for (int i = size; i > index; i--) {
elementData[i] = elementData[i - 1];
}
elementData[index] = e;
size++;
}
// 인덱스 위치의 요소를 반환한다.
@SuppressWarnings("unchecked")
public E get(int index) {
return (E) elementData[index];
}
// 인덱스 위치의 값을 새 값으로 바꾸고, 이전 값을 반환한다.
@SuppressWarnings("unchecked")
public E set(int index, E element) {
E old = (E) elementData[index];
elementData[index] = element;
return old;
}
// 지정 위치의 요소를 삭제하고, 뒤의 요소들을 한 칸씩 당겨 빈 공간을 메운다.
@SuppressWarnings("unchecked")
public E remove(int index) {
E old = (E) elementData[index];
for (int i = index; i < size - 1; i++) {
elementData[i] = elementData[i + 1];
}
elementData[--size] = null;
return old;
}
// 리스트에서 처음 만나는 요소의 인덱스를 반환한다.
public int indexOf(E o) {
for (int i = 0; i < size; i++) {
if (o.equals(elementData[i])) {
return i;
}
}
return -1;
}
// 배열 상태와 크기를 출력한다.
@Override
public String toString() {
Object[] actual = Arrays.copyOf(elementData, size);
return Arrays.toString(actual) +
" size=" + size +
", capacity=" + elementData.length;
}
}
주요 메서드별 상세 설명
- grow()
내부 배열이 꽉 찼을 때 호출된다.- 현재 용량(oldCapacity)을 읽어온다.
- 두 배 크기(newCapacity = oldCapacity * 2)를 계산한다.
- Arrays.copyOf로 새 배열을 만들고 기존 데이터를 한 번에 복사한 뒤, 참조를 교체한다.
→ 시간 복잡도 O(n), 하지만 확대 횟수가 줄어들어 암묵적 평균 O(1)

- add(E e)
리스트 끝에 요소를 추가한다.- size == elementData.length로 용량 부족 여부를 검사한다.
- 부족하면 grow()로 배열을 확장한다.
- elementData[size++] = e로 요소를 대입하고 크기를 1 증가시킨다.
→ 보통 O(1), (확장 시) O(n)
- add(int index, E e)
지정한 위치에 요소를 삽입한다.- 끝에 추가하듯 용량을 검사하고 필요 시 grow() 호출.
- for 루프를 통해 index부터 size-1까지 모든 요소를 한 칸씩 뒤로 이동시켜 빈 공간을 만든다.
- elementData[index] = e로 값을 넣고 size++.
→ 항상 O(n) (shift 비용)

- remove(int index)
지정한 위치의 요소를 삭제하고 반환한다.- 삭제할 값을 임시 변수(old)에 저장한다.
- for 루프로 index+1부터 size-1까지 요소를 한 칸씩 앞으로 당겨 빈칸을 메운다.
- elementData[--size] = null로 마지막 칸을 null 처리해 가비지 컬렉터가 회수하도록 한다.
- old를 반환한다.
→ O(n) (shift 비용)
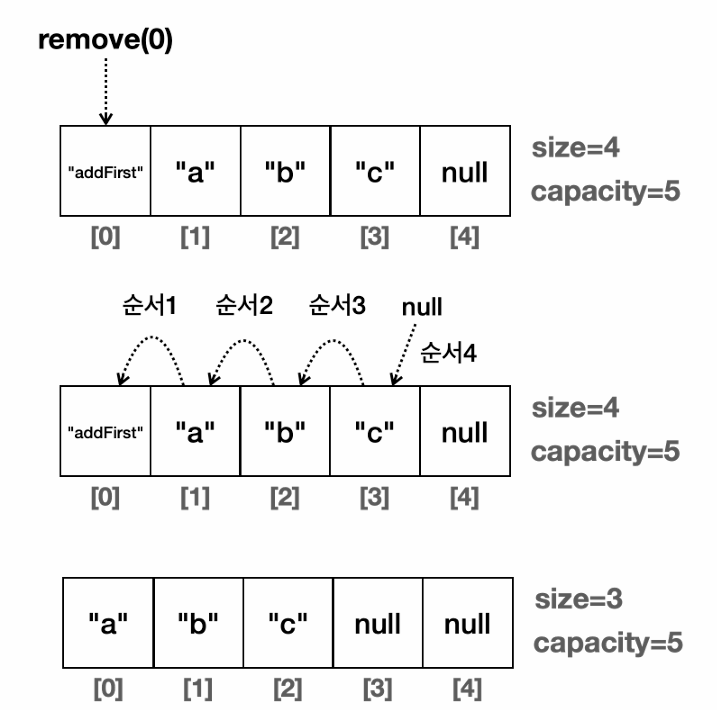
이 구현은 배열의 근본적 불편함을 자동 확장과 내부 로직으로 해결한다. 크기를 미리 정해야 하는 문제는 grow()가 배열이 꽉 찰 때마다 두 배로 늘려 주므로 더 이상 고민할 필요가 없고, 복사 코드를 수동으로 작성하던 수고는 Arrays.copyOf 한 줄로 대체된다. 이 과정은 배열 복사 비용 O(n)을 수반하지만, 한 번 확장할 때마다 두 배 용량이 확보되므로 암묵적으로 평균 O(1)의 추가 비용을 유지한다. 중간 삽입과 삭제 시 요소 이동 로직 역시 add(index, e)와 remove(index) 내부에서 자동으로 수행되며, 이때는 항상 O(n)의 시간이 든다. 결국 “크기 고정”과 “수동 복사·이동”이라는 배열의 단점을 MyArrayList가 깔끔하게 해소한다.
ArrayList의 빅오 정리
- 마지막에 추가: 평균 O(1)
- 앞·중간에 추가: O(n)
- 마지막에 삭제: O(1)
- 앞·중간에 삭제: O(n)
- 인덱스 조회: O(1)
- 검색(indexOf): O(n)
MyLinkedList: 연결 리스트 기반 리스트 구현
연결 리스트는 각 데이터를 노드 객체에 담고, 노드 간 참조만 바꾸는 방식으로 삽입·삭제를 처리한다. 중간 삽입과 삭제는 O(1)에 가깝지만, 원하는 위치를 찾기 위해 순회하는 과정이 필요해 O(n)의 시간이 든다.
코드 구현:
package collection.link;
public class MyLinkedList<E> {
private static class Node<E> {
E item;
Node<E> next;
Node(E item) { this.item = item; }
}
private Node<E> first; // 리스트의 첫 노드
private int size = 0; // 요소 개수
// 맨 뒤에 요소 추가: 리스트가 비어 있으면 first에, 아니면 마지막 노드 뒤에 연결
public void add(E e) {
Node<E> node = new Node<>(e);
if (first == null) {
first = node;
} else {
Node<E> cur = first;
while (cur.next != null) {
cur = cur.next;
}
cur.next = node;
}
size++;
}
// 지정한 위치에 요소 삽입: 맨 앞이면 first 변경, 아니면 이전 노드를 찾아 링크만 재구성
public void add(int index, E e) {
Node<E> node = new Node<>(e);
if (index == 0) {
node.next = first;
first = node;
} else {
Node<E> prev = getNode(index - 1);
node.next = prev.next;
prev.next = node;
}
size++;
}
// index 위치의 노드를 순회하여 찾아 반환한다.
private Node<E> getNode(int index) {
Node<E> cur = first;
for (int i = 0; i < index; i++) {
cur = cur.next;
}
return cur;
}
// 인덱스 조회
public E get(int index) {
return getNode(index).item;
}
// 인덱스 위치 요소를 새 값으로 교체
public E set(int index, E element) {
Node<E> node = getNode(index);
E old = node.item;
node.item = element;
return old;
}
// 지정 위치 요소 삭제: 이전 노드의 링크만 건너뛰도록 변경
public E remove(int index) {
if (index == 0) {
E old = first.item;
first = first.next;
size--;
return old;
}
Node<E> prev = getNode(index - 1);
Node<E> cur = prev.next;
E old = cur.item;
prev.next = cur.next;
size--;
return old;
}
// 검색
public int indexOf(E o) {
Node<E> cur = first;
int idx = 0;
while (cur != null) {
if (o.equals(cur.item)) return idx;
cur = cur.next;
idx++;
}
return -1;
}
@Override
public String toString() {
StringBuilder sb = new StringBuilder("[");
Node<E> cur = first;
while (cur != null) {
sb.append(cur.item);
if (cur.next != null) sb.append("->");
cur = cur.next;
}
sb.append("] size=").append(size);
return sb.toString();
}
}
주요 메서드 설명:
add(E e)
- 리스트 끝에 요소를 추가한다.
- first == null이면 새 노드를 first에 연결하고, 아니면 first부터 순회하여 마지막 노드까지 간 뒤 next에 새 노드를 연결한다.
- size++로 요소 개수를 증가시킨다.
→ 시간 복잡도: O(n) (항상 마지막 노드까지 순회)
add(int index, E e)
- 지정한 위치에 요소를 삽입한다.
- index == 0이면 새 노드를 first로 설정하고 기존 first를 next에 연결한다.
- 그렇지 않으면 getNode(index – 1)로 이전 노드를 찾는다(순회 O(n)).
- 새 노드의 next를 이전 노드의 next로 설정하고, 이전 노드의 next를 새 노드로 연결한다.
- size++로 요소 개수를 증가시킨다.
→ 시간 복잡도: O(n) (위치 탐색 O(n) + 링크 재구성 O(1))



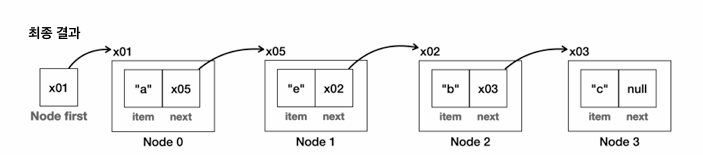
get(int index)
- getNode(index)로 index 위치의 노드를 찾아 item을 반환한다.
- getNode는 first부터 index만큼 next를 따라가기 때문에 O(n)이다.
→ 시간 복잡도: O(n)
set(int index, E element)
- getNode(index)로 해당 노드를 찾아 item을 새 값으로 교체하고, 이전 값을 반환한다.
→ 시간 복잡도: O(n) (위치 탐색)
remove(int index)
- index == 0이면 first를 first.next로 바꾸고 size-- 후 이전 first.item을 반환한다.
- 그렇지 않으면 getNode(index – 1)로 이전 노드를 찾고, prev.next = prev.next.next로 링크를 건너뛴 뒤 size-- 하고 삭제된 값을 반환한다.
→ 시간 복잡도: O(n) (위치 탐색 O(n) + 링크 재구성 O(1))


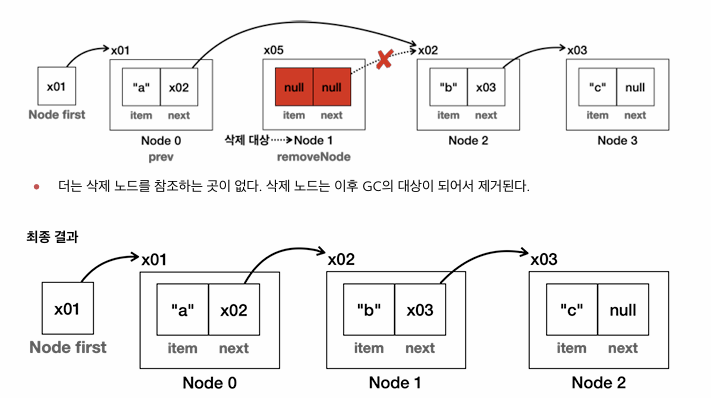
indexOf(E o)
- first부터 next를 따라가며 item.equals(o)를 확인한다.
- 일치하면 그때까지 순회한 인덱스를 반환하고, 끝까지 못 찾으면 –1을 반환한다.
→ 시간 복잡도: O(n)
개선된 점을 분기하여 정리하면 다음과 같다:
- 용량 걱정 해소
- 배열은 생성 시 크기를 미리 정해야 했지만, 연결 리스트는 노드를 동적으로 할당하므로 “용량 부족”이나 “남는 공간 낭비”에 대한 고민이 사라진다.
- 중간 삽입·삭제 비용 절감
- 배열에서 중간에 데이터를 넣거나 뺄 때는 뒤쪽 요소를 모두 이동시켜야 하지만, 연결 리스트는 해당 노드의 앞·뒤 링크만 재구성하면 되므로 삽입·삭제 자체는 O(1)에 가깝게 수행된다.
- 메모리 단편화 완화
- 배열은 연속된 메모리 블록을 요구해 대용량일수록 얻기 어려울 수 있지만, 연결 리스트는 분산된 메모리 공간에 노드를 할당하므로 단편화 문제를 줄여준다.
- 코드 단순화 및 유지보수성 향상
- 요소 이동(shift) 루프 없이 링크 조작만으로 삽입·삭제 로직을 구현할 수 있어, 코드가 직관적이고 버그 발생 가능성이 낮아진다.
- 처음·가운데 삽입 우수
- 배열은 앞쪽에 추가/삭제할 때 매번 모든 요소를 밀지만, 연결 리스트는 항상 동일하게 링크만 바꾸므로 앞쪽 연산에서도 효율적이다.
이처럼 연결 리스트는 배열 기반 리스트의 ‘고정 크기’, ‘중간 이동 비용’이라는 근본적 단점을 효과적으로 해소한다.
시간 복잡도 비교:
직접 구현한 MyArrayList(배열 기반)와 MyLinkedList(단일 연결 리스트)의 주요 연산별 시간 복잡도는 다음과 같다.
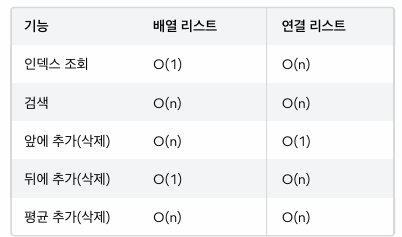
배열 리스트는 인덱스를 통해 바로 접근할 수 있어 “추가/삭제 위치 탐색”이 O(1)으로 빠르다. 그러나 “추가나 삭제 이후에 요소를 한 칸씩 밀거나 당기는” 작업이 필요해 그 비용이 O(n)으로 크다.
반면 연결 리스트는 노드를 순회해 원하는 위치(O(n))를 찾아야 하므로 탐색 속도는 느리다. 하지만 삽입·삭제 이후에는 앞뒤 노드의 참조만 재구성하면 되므로 그 자체는 O(1)에 가깝다.
예를 들어 앞쪽에 요소를 추가할 때,
- 배열 리스트: 모든 요소를 오른쪽으로 한 칸씩 밀어야 하므로 O(n)
- 연결 리스트: 단지 첫 노드의 참조만 바꾸면 되므로 O(1)
마지막에 요소를 추가할 때는,
- 배열 리스트: 인덱스로 바로 마지막 위치를 찾아 O(1)
- 연결 리스트(단일): 마지막 노드를 찾기 위해 매번 순회해야 하므로 O(n)
(하지만 노드 연결 자체는 O(1))
결국
- 데이터 조회가 많고 뒤쪽 추가/삭제가 빈번하다면 배열 리스트를 사용하고,
- 앞쪽 또는 중간 삽입/삭제가 많을 때는 연결 리스트가 유리하다.
단일 연결 리스트 vs 이중 연결 리스트
지금까지 구현한 MyLinkedList는 단일 연결 리스트로, 각 노드가 다음 노드만 가리킨다.
이 경우 “마지막 노드”를 찾으려면 매번 순회해야 하는 단점이 있다. 이를 해결한 것이 이중 연결 리스트다.
public class Node<E> {
E item;
Node<E> next; // 다음 노드 참조
Node<E> prev; // 이전 노드 참조
}
이중 연결 리스트는
- 각 노드가 앞·뒤를 모두 가리키므로,
- 뒤쪽 삽입/삭제 시에도 tail(마지막 노드) 참조만 알면 O(1)에 처리할 수 있다.
자바 표준 LinkedList는 바로 이 구조를 사용하며, first와 last를 모두 유지해 “앞쪽 삽입·삭제”와 “뒤쪽 삽입·삭제”를 모두 O(1)에 가깝게 지원한다.
마무리하며:
우리는 먼저 배열의 고정 크기와 수동 복사·이동의 번거로움을 MyArrayList의 자동 용량 확장과 내부 add/remove 로직으로 대체해 보았다.
이어서 중간 삽입·삭제 시 O(n)의 이동 비용을 단일 연결 리스트인 MyLinkedList의 링크 조작만으로 O(1)에 가깝게 처리하는 방법을 직접 구현하고, 빅오 관점에서 두 구조의 차이를 명확히 살펴보았다.
다음 장에서는 자바 표준 라이브러리에 이미 구현되어 있는 ArrayList와 LinkedList를 사용해 직접 구현한 성능에 비해 얼마나 차이나는지, 또한 표준 라이브 러리 기능에 대해서도 살펴볼 것이다.
감사합니다.
'자바' 카테고리의 다른 글
| [JAVA] Set 인터페이스에 대하여 (3) (1) | 2025.07.20 |
|---|---|
| [JAVA] List에 인터페이스에 대하여 (2) (5) | 2025.07.18 |
| [JAVA] 자바 제네릭 메서드와 와일드카드, 그리고 타입 이레이저 (1) | 2025.07.16 |
| [JAVA] 제네릭이 필요한 이유 (1) | 2025.07.14 |
| [JAVA] 예외 처리4 -실무 (4) | 2025.07.12 |
