문제 링크:
난이도: 골드 3
문제:
하나 이상의 연속된 소수의 합으로 나타낼 수 있는 자연수들이 있다. 몇 가지 자연수의 예를 들어 보면 다음과 같다.
- 3 : 3 (한 가지)
- 41 : 2+3+5+7+11+13 = 11+13+17 = 41 (세 가지)
- 53 : 5+7+11+13+17 = 53 (두 가지)
하지만 연속된 소수의 합으로 나타낼 수 없는 자연수들도 있는데, 20이 그 예이다. 7+13을 계산하면 20이 되기는 하나 7과 13이 연속이 아니기에 적합한 표현이 아니다. 또한 한 소수는 반드시 한 번만 덧셈에 사용될 수 있기 때문에, 3+5+5+7과 같은 표현도 적합하지 않다.
자연수가 주어졌을 때, 이 자연수를 연속된 소수의 합으로 나타낼 수 있는 경우의 수를 구하는 프로그램을 작성하시오.
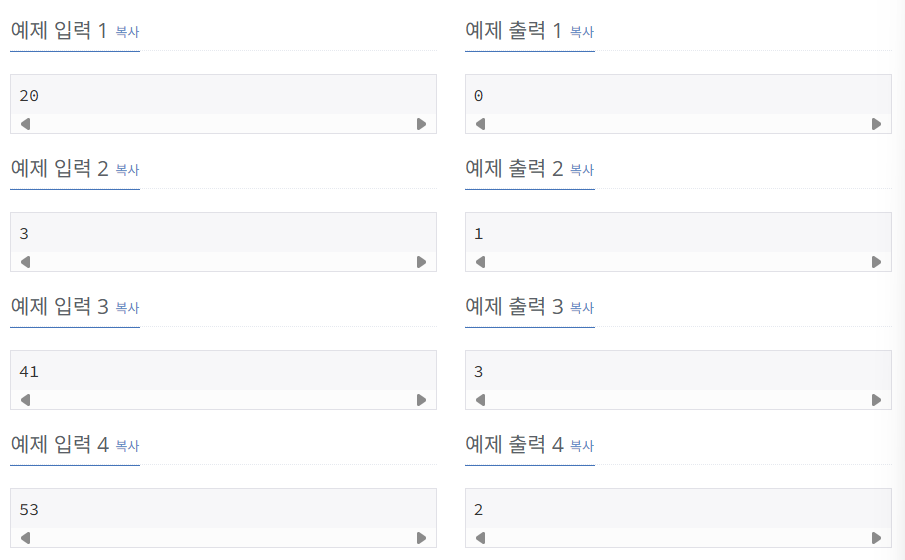
입력:
첫째 줄에 자연수 N이 주어진다. (1 ≤ N ≤ 4,000,000)
출력:
첫째 줄에 자연수 N을 연속된 소수의 합으로 나타낼 수 있는 경우의 수를 출력한다.
문제 이해:
이 문제는 자연수 N이 주어졌을 때, 그 수를 연속된 소수의 합으로 표현할 수 있는 경우의 수를 구하는 문제이다.
예를 들어, N = 41인 경우를 살펴보면,
- 41 = 2 + 3 + 5 + 7 + 11 + 13
- 41 = 11 + 13 + 17
- 41 = 41
즉, 세 가지 방법으로 41을 연속된 소수의 합으로 나타낼 수 있다.
구현 방향:
소수와 관련된 문제는 대부분 에라토스테네스의 체를 사용한다.
이 알고리즘은 2부터 시작하여, 특정 수의 배수를 모두 제거(또는 false로 표시)함으로써 소수를 효율적으로 판별할 수 있다.
따라서 2부터 N의 최대값인 4,000,000까지 반복하며, 각 인덱스에 해당하는 수가 소수인지를 판별하고, 그 배수들을 모두 false로 세팅하면 된다.
연속된 소수의 합으로 N을 표현할 수 있는 경우의 수를 구하기 위해 처음에는 적절한 알고리즘을 떠올리지 못했으나, 자료를 찾아본 결과 투 포인터(Two Pointers) 알고리즘을 사용하는 것이 적합하다는 것을 알게 되었다.
이 알고리즘은 주로 다음과 같은 상황에서 활용된다.
- 두 수의 합, 차, 곱, 조건 비교
- 연속된 부분합
- 중복 없는 부분 문자열 탐색
- 슬라이딩 윈도우 문제
투 포인터 알고리즘의 핵심은 두 개의 포인터(left, right)를 이용해 구간의 합을 유지하며, 합이 너무 작으면 오른쪽 포인터를 이동시키고, 합이 너무 크면 왼쪽 포인터를 이동시키는 방식이다.
예) N=7, 소수=[2,3,5,7,…] →
① left=0,right=0,sum=2(작음)→right++ →
② left=0,right=1,sum=5(작음)→right++ →
③ left=0,right=2,sum=10(큼)→left++ →
④ left=1,right=2,sum=8(큼)→left++ →
⑤ left=2,right=2,sum=5(작음)→right++ →
⑥ left=2,right=3,sum=12(큼)→left++ →
⑦ left=3,right=3,sum=7(정답)→count++.
이를 코드로 그대로 구현하면 다음과 같다.
정답코드:
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
public class Main {
static boolean []primes= new boolean[4000001];
static int N;
static int result=0;
//소수만 true 활성화
public static void primesSet(){
primes[1]=false;
for(int i=2; i<4000001; i++){
if(!primes[i]) continue;
else{
for(int j=2*i; j<4000001; j+=i){
primes[j]=false;
}
}
}
}
//투포인터 알고리즘을 이용하여 해결
public static void solve(){
int target=N;
int left=2;
int sum=0;
boolean flag=true;
for(int R=2; R<=N; R++){
if(primes[R]){
sum += R;
flag=true;
}
//왼쪽 한칸 전진
while (sum > target && left <= R){
sum -= left;
for(int i=left+1; i<=N; i++){
if(primes[i]){
left=i;
break;
}
}
}
//소수의 합들이 입력한 N이면 개수 증가
if (flag && sum == target){
result++;
flag=false;
}
}
}
public static void main(String[] args) throws IOException {
//초기 세팅
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
N=Integer.parseInt(br.readLine());
Arrays.fill(primes, true);
//초기 세팅 끝
//에라토스테네스의 체 적용하여 소수만 ture
primesSet();
//탐색 시작
solve();
//결과 출력
System.out.println(result);
}
}
마무리하며:
코딩 테스트를 연습하면서 투 포인터 방식의 문제는 처음 풀어본 것 같다.
하지만 이론 자체가 복잡하거나 어려운 개념은 아니기 때문에, 꾸준히 연습하면 금방 익숙해질 것 같다.
특히 처음 투 포인터 알고리즘을 접하는 사람들에게는 이 문제가 좋은 연습문제가 될 것이다.
감사합니다.
'코딩 테스트' 카테고리의 다른 글
| [백준] 3273 두 수의 합 (JAVA) (0) | 2025.10.21 |
|---|---|
| [백준] 13144 List of Unique Numbers (JAVA) (0) | 2025.10.20 |
| [백준] 1202 보석 도둑 (JAVA) (0) | 2025.10.16 |
| [백준] 1931 회의실 배정 (JAVA) (0) | 2025.10.14 |
| [백준] 14469 소가 길을 건너간 이유 3 (JAVA) (0) | 2025.10.13 |
